| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Python
- 멘델레이
- 스틸브릿지
- 클러스터링
- 파이썬
- Desktop
- 머신러닝
- github
- ppt
- 포스코
- 비지도학습
- matplotlib
- CAD
- 열역학
- 모깎이
- 군집화
- 매트랩
- PEMFC
- git
- 기계공학
- mendeley
- Fusion 360
- matlab
- 연료전지
- 윈도우
- simulink
- 파워포인트
- reference manager
- 시뮬링크
- 포스코인턴
- Today
- Total
신군의 역학사전
삼각함수의 직교성 (Orthogonality of Trigonometric System) 본문
삼각함수의 직교성 (Orthogonality of Trigonometric System)
긔눈 2024. 12. 4. 12:00이번 포스팅에서는 삼각함수의 중요한 성질 중 하나인 직교성에 대해 정리해보도록 하겠습니다. 차후 푸리에 급수를 전개해나갈 때 기본이 되는 내용으로, 겸사겸사 가볍게 유도해보고 지나가면 좋을 듯 합니다.
1. 함수의 직교성 (Orthogonality)
'직교'라는 용어는 예전부터 많이 들어왔을 테지만, 이를 수식화하기 시작했던 것은 고등학생 때 '벡터의 내적'을 다루면서부터이지 않을까 싶습니다. 당시 a벡터와 b벡터가 수직이라면, 내적은 0이 됨을 배웠었습니다.
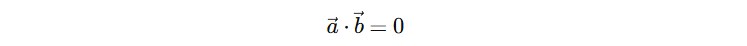
이는 함수에도 유사하게 생각할 수 있는데요, 함수의 직교성은 아래와 같이 정의할 수 있습니다.

즉 '[a,b]에서 f와 g라는 함수의 적분값이 0이라면, 해당 구간 내에서 두 함수는 직교한다'라고 정의합니다.
2. 삼각함수의 직교성 (Orthogonality of Trigonometric System)
푸리에 급수에서는 주로 삼각함수를 다루기 때문에, 삼각함수의 성질에 대해 정리할 필요가 있습니다. 기본적으로 Sine, Cosine함수는 아래의 식을 만족하는데요

이를 바탕으로 삼각함수의 직교성에 대해 전개해 보겠습니다. 푸리에 급수에서는 기본적으로 Sine, Cosine wave의 Sum을 다루기 때문에, 직교성을 볼 때 아래의 3가지 경우에 대해 생각해볼 수 있습니다.
1. 코사인함수 x 코사인함수
2. 사인함수 x 사인함수
3. 사인함수 x 코사인함수
2-1) Cosine X Cosine function

[-Pi, Pi]구간에서 Cosine함수 간의 곱의 적분은 n과 m이 다를 때 0을 만족합니다. 즉, 기본주기가 다른 2개의 Cosine함수의 경우 [-Pi, Pi]에서 직교합니다. 관련한 유도과정은 아래와 같습니다.
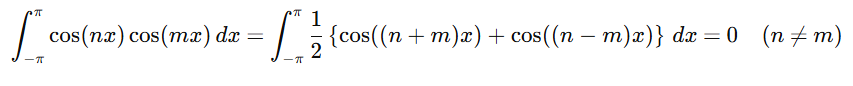
n과 m이 다를 경우, Cosine함수만 적분기호 내에 남기 때문에, 구간내에서 적분값은 0이 됩니다.

반대로 n과 m이 같을 경우, cos값이 1로 정리되기 때문에 상수값이 남게됩니다. 즉, Cos함수는 자기자신과 해당 구간 내에서 직교한다 라고 볼 수 없습니다. 다만, 다른 Cosine 함수 간에는 직교성을 띈다고 볼 수 있습니다.
2-2) Sine X Sine function

Sine 함수 간의 직교성 역시, 2-1의 경우와 유사합니다. 기본 주기가 다른 경우 직교성을 띄지만, 그렇지 않은 경우 직교성을 띄지 않습니다. 자세한 유도과정은 아래와 같습니다. 삼각함수의 곱을 합으로 바꿔주는 공식을 활용하면 쉽게 유도할 수 있습니다.


정리하자면, Sine 함수는 자기자신과 해당 구간 내에서 직교한다 라고 볼 수 없지만, 기본 주기가 다른 Sine함수 간에는 직교성을 띈다고 볼 수 있습니다.
2-3) Sine X Cosine function

반면, Sine함수와 Cosine 함수간의 직교성을 살펴보면, 조금의 차이점이 있습니다. 이 경우, 기본주기가 같은 경우 역시 직교성을 띄는데요, 이는 아래의 유도과정에서 이유를 확인할 수 있습니다.
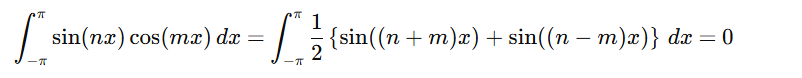
sine과 cosine의 곱은 sine 끼리의 합으로 정리가 가능한데, sine함수의 경우 sin(0) = 0을 만족하기 때문에 이전에 Cosine 함수가 Cos(0) = 1 로 정리되었던 것과 차이가 있습니다. 즉, 추가적인 상수항이 남지 않기 때문에, 어떤 경우에도 직교성을 띄게 됩니다.
따라서 Sine & Cosine 함수는 자기자신을 제외하면, [-Pi, Pi]구간에서 직교성을 띈다 라고 정리할 수 있습니다.
