| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- matplotlib
- 멘델레이
- 클러스터링
- 포스코인턴
- 기계공학
- 모깎이
- 스틸브릿지
- PEMFC
- CAD
- 연료전지
- git
- reference manager
- 파워포인트
- 포스코
- Fusion 360
- 시뮬링크
- Desktop
- 윈도우
- 군집화
- Python
- github
- matlab
- 파이썬
- ppt
- mendeley
- 비지도학습
- 열역학
- simulink
- 매트랩
- 머신러닝
- Today
- Total
신군의 역학사전
[ML] 비지도학습 - 계층적 군집화(Hierarchical Clustering) 본문
[ML] 비지도학습 - 계층적 군집화(Hierarchical Clustering)
긔눈 2025. 3. 31. 12:001. 계층적 군집화(Hierarchical Clustering)
계층적 군집화(Hierarchical Clustering)는 데이터 간의 유사성을 기반으로, 각 데이터가 개별 군집에서 시작하여 반복적인 병합 또는 분할 과정을 통해 계층적인 트리 구조(Dendrogram)를 형성하는 비지도학습 기법이다. K-means Clustering과는 달리 클러스터의 수를 사용자가 미리 지정해주지 않아도 된다는 장점이 있으며, 트리 구조를 통해 의미있는 분류 체계를 도출할 수 있다(트리구조의 높이로 taxonomy를 찾아낼 수도 있다). 최종적으로 생성된 덴드로그램을 바탕으로 사용자가 적절한 Cutting Point를 정해 클러스터 수를 나누게 된다. 아래의 그림을 예로들면, 수직선을 어디에 긋냐에 따라 최종 클러스터의 수가 결정된다.
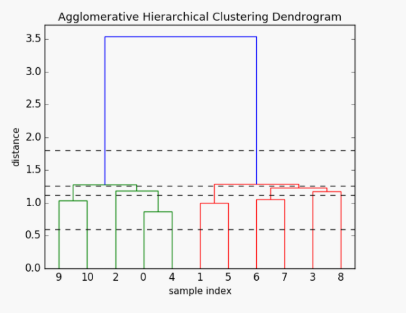
그래서 K-means Clustering으로 대표되는 분할 군집화(Partitional Clustering)과의 차이점을 정리해보면 아래의 그림과 같다. 분할 군집화의 경우 중첩없는 독립된 클러스터를 반환하는 반면, 계층적 군집화 기법은 데이터의 유사성을 반영하는 중첩된 클러스터 구조를 반환해준다는 특징이 있다.
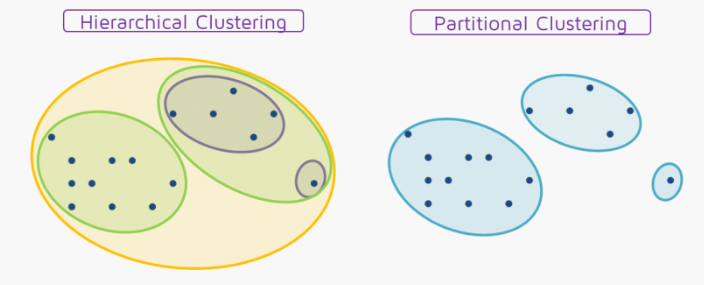
2. Types of Linkage
계층적 군집화에서, 두 군집간의 거리(유사도)를 정의하는 지표로 Linkage라는 개념을 활용한다. Single, Complete, Average, Centroid의 4가지 Linkage를 주로 활용하는데, 각각 아래와 같다. Linkage를 계산할 때 주로 유클리디언 거리를 활용하나 절대적인건 아니고, 맨해튼 거리(Manhattan Distance), 코사인 거리(Cosine Distance), 자카드 거리(Jacaard Distance) 등 여러 계산방법이 있다. 이는 아래에서 볼 sklearn 내장함수에 metric으로 지정해줄 수 있다.
2-1. Single Linkage : 클러스터간 최소거리
2-2. Complete Linkage : 클러스터간 최대거리
2-3. Average Linkage : 클러스터간 평균거리
2-4. Centroid Linkage : 클러스터의 중심(Centroid)간 거리
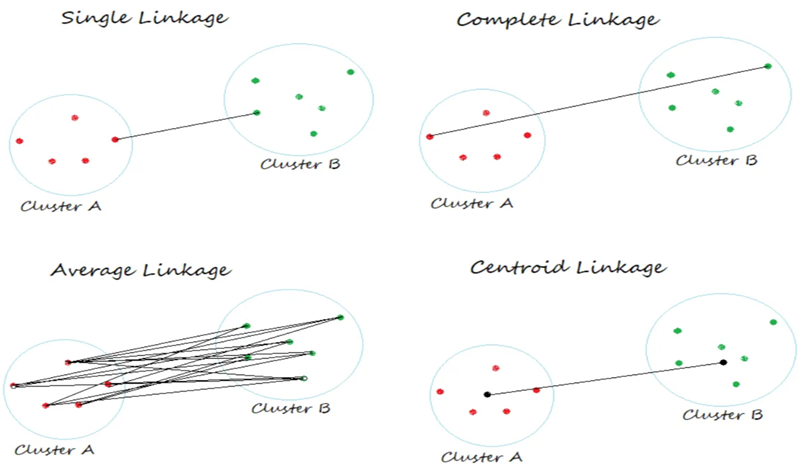
그리고 당연하게도(?) 어떤 Linkage를 사용하는지에 따라 클러스터링 결과가 달라질 수 있다.
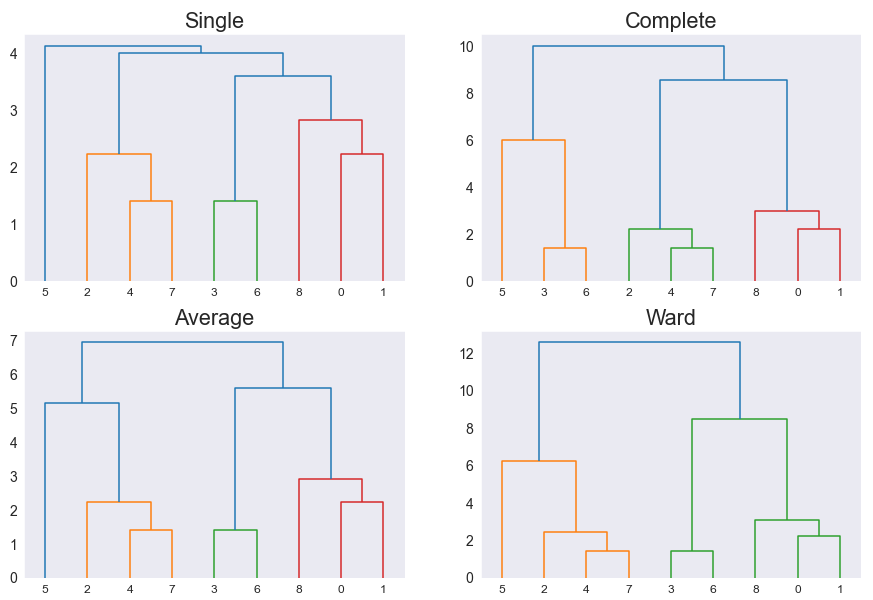
3. Types of Hierarchical Clustering
계층적 군집화에는 크게 2가지 방법이 있다. 하나의 거대군집으로부터 시작해 세부 군집으로 나누며 진행하는 분할 계층 군집화(Divisive Hierarchical Clustering)과, 각 개별군집으로부터 시작해 거대군집 구조를 형성해나가는 병합 계층 군집화(Agglomerative Hierarchical Clustering). 쉽게 정리하면 Top-Down이냐 Bottom-Up이냐의 차이다.
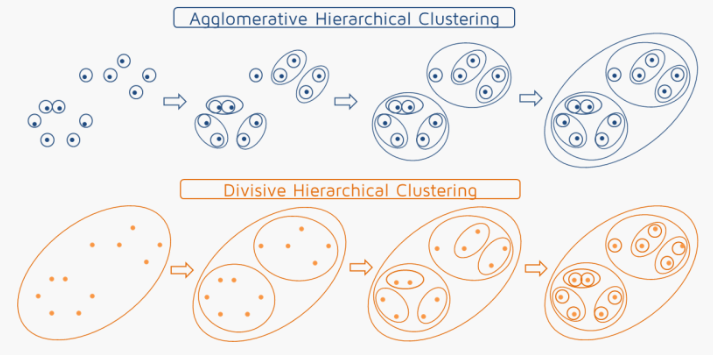
3-1. Agglomerative Clustering
병합 계층 군집화는 각 데이터 포인트를 개별 군집으로 할당하고, 유사한 군집을 병합해나가는 군집화 방식으로, 몇가지 세부방식이 있다. 앞서 4가지 Linkage에 대해 정리했는데, 특정 Linkage 기준 가장 가까운 클러스터를 병합해나가는 방식과, 클러스터 병합 후 군집 내 오차제곱합의 증가량이 최소가 되는 군집 쌍을 선택하는 Ward's Method 등이 있다. 즉, Ward's Method에 따르면 병합전 SSE(Sum of Squared Error)가 8이고, 병합 후 SSE가 15,20,25가 되는 선택지들이 있다면 15가 되는 클러스터를 병합한다. 이때 병합 전후 SSE의 차이를 Ward Distance라고도 하며, 이 경우 15-8=7이 된다. 아래는 Agglomerative Clustering에 대한 Pseudocode.

3-2. Divisive Clustering
Divisive는 Agglomerative와는 반대로 가장 큰 Linkage를 가진 클러스터를 거대 군집으로부터 분할하는 방식으로 클러스터링이 이루어진다. 아래는 이에 대한 Pseudocode.

4. Practical Issue
계층적 군집화에서 고려해야할 Practical Issue들을 정리하면 아래와 같다.
4-1. 변수 스케일링(Scaling)의 중요성
변수마다 측정 단위나 분포가 다를 수 있어, 클러스터링 전에 표전화 등의 스케일링을 적용하는 것이 일반적이나, 스케일링 방식에 따라 결과가 크게 달라지므로 어떤 방식의 스케일링을 적용해야할지 결정해야 한다.
4-2. 군집 간의 거리(Linkage) 혹은 불일치도(Disimilarity) 측정 방법
데이터 특성에 따라 적절한 거리함수를 선택해야 한다.
4-3. 클러스터 수 결정 문제
K-means Clustering과 마찬가지로 정해진 정답이 없기 때문에, 문제 상황과 해석의 목적에 따라 최적 클러스터 수는 달라진다. 엘보우 메소드 등에 따라 최적 클러스터 수를 결정할 수 있을 듯.
4-4. 변수 선택 문제
어떤 변수(Feature)를 클러스터링에 포함하느냐에 따라 결과가 달라지므로, 불필요한 변수는 제거되어야 한다.
5. 계층적 군집화 구현하기
우선 sklearn에서는 AgglomerativeClustering만 내장함수로 지원한다. Divisive의 경우 따로 지원하고 있지 않은데, 이유는 아마도.. 계산복잡도가 크고 계산 안정성이 Agglomerative에 비해 떨어지기 때문인 듯 하다.
어쨌든 필요한 모듈은 아래와 같다. sklearn에서 지원하는 AgglomerativeClustering함수가 있으며, scipy에서 지원하는 linkage와 dendrogram 등이 있다. 실제로 계층적 군집화 자체는 linkage함수만으로 진행할 수 있고, dendrogram으로 이를 시각화한 후, 최적 클러스터를 사용자가 결정해 AgglomerativeClustering함수를 활용해 클러스터링을 진행한다.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import AgglomerativeClustering
from scipy.cluster.hierarchy import linkage, dendrogram
plt.rcParams['font.family'] = 'Times New Roman'아래는 데이터셋을 임의로 만들어주는 과정이며, 최적 클러스터수는 3개가 되도록 랜덤하게 생성해주었다.
np.random.seed(42)
X1 = np.random.normal(loc=0.0, scale=1.0, size=(50, 2))
X2 = np.random.normal(loc=5.0, scale=1.0, size=(50, 2))
X3 = np.random.normal(loc=(0.0, 5.0), scale=1.0, size=(50, 2))
X = np.vstack((X1, X2, X3))Linkage라는 함수로 해당 데이터 셋에 대해 계층적 군집화를 진행할 수 있으며, 이때 군집화 method를 지정할 수 있다. 앞서봤던 Single, Average, Centroid, Ward 등을 인자로 전달할 수 있는데, 해당 예시에선 ward로 지정했다.
https://docs.scipy.org/doc/scipy/reference/generated/scipy.cluster.hierarchy.linkage.html
linkage — SciPy v1.15.2 Manual
For method ‘single’, an optimized algorithm based on minimum spanning tree is implemented. It has time complexity \(O(n^2)\). For methods ‘complete’, ‘average’, ‘weighted’ and ‘ward’, an algorithm called nearest-neighbors chain is imple
docs.scipy.org
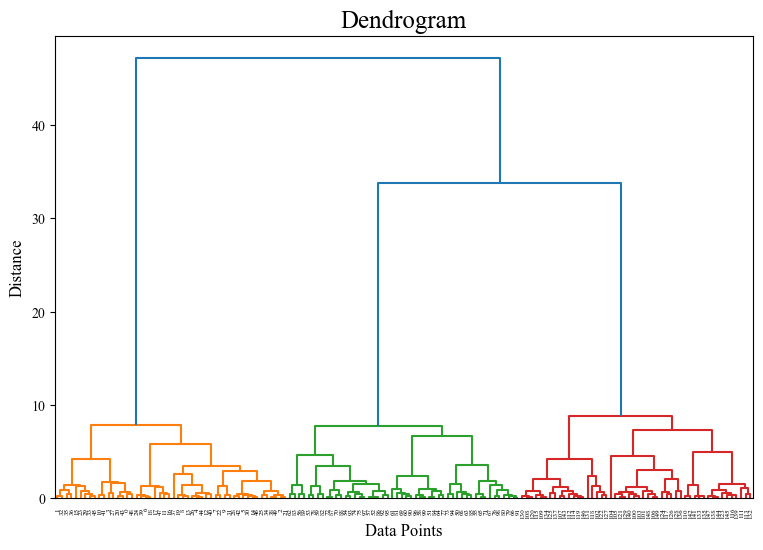
그리고 덴드로그램으로 시각화를 해주면 아래의 결과와 같다.
Z = linkage(X, method='ward')
plt.figure(figsize=(9, 6))
dendrogram(Z)
plt.title("Dendrogram", fontsize=18)
plt.xlabel("Data Points", fontsize=12)
plt.ylabel("Distance", fontsize=12)
plt.show()해당 덴드로그램을 볼 때, y축(Distance) 기준 하늘색 라인을 따라 자르는게 가장 합리적인 선택으로 보인다. 하위 계층은 클러스터별 분류가 가깝기 때문. 물론 이는 데이터셋을 3개 군집에 적합하도록 생성하여 볼 수 있는 결과다.
따라서, 최종 라벨링을 클러스터 수가 3개가 되도록 해주면 아래와 같고
model = AgglomerativeClustering(n_clusters=3, metric='euclidean', linkage='ward')
model.fit(X)
labels = model.labels_
print("Cluster labels:\n", labels)최종적으로 3개의 클러스터로 나뉜것을 확인할 수 있다.

Reference
[1] : https://quantdare.com/hierarchical-clustering/
[2] : https://harikabonthu96.medium.com/single-link-clustering-clearly-explained-90dff58db5cb
[3] : https://www.learndatasci.com/glossary/hierarchical-clustering/
[4] : https://cs.joensuu.fi/pages/oili/PR/?a=Some__Material&b=Hierarchical__Clustering
'Machine Learning > Unsupervised Learning' 카테고리의 다른 글
| [ML] 비지도학습 - 차원의 저주(Curse of Dimensionality)와 차원 축소 기법(Dimensionality Reduction) (0) | 2025.04.14 |
|---|---|
| [ML] 비지도학습 - DBSCAN (0) | 2025.04.07 |
| [ML] 비지도학습 - K-평균 군집화(K-means Clustering) (0) | 2025.03.24 |
| [ML] 비지도학습 - 클러스터링 개요(Clustering - Overview) (0) | 2025.03.17 |





