| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 머신러닝
- CAD
- Desktop
- matplotlib
- simulink
- 모깎이
- github
- matlab
- 포스코인턴
- Python
- 연료전지
- mendeley
- 열역학
- git
- 시뮬링크
- Fusion 360
- 기계공학
- PEMFC
- 스틸브릿지
- reference manager
- 윈도우
- 파워포인트
- ppt
- 매트랩
- 군집화
- 멘델레이
- 비지도학습
- 클러스터링
- 포스코
- 파이썬
- Today
- Total
신군의 역학사전
[ML] 비지도학습 - K-평균 군집화(K-means Clustering) 본문
[ML] 비지도학습 - K-평균 군집화(K-means Clustering)
긔눈 2025. 3. 24. 12:001. K-평균 군집화(K-means Clustering)란?
K-means Clustering은 분할 군집화(Partitional Clustering) 알고리즘 중 하나로, 미리 지정된 K개의 클러스터로 데이터를 나누어 각 클러스터 내에서 데이터가 최대한 서로 가깝게 되도록 하는 것을 목표로 한다. 이를 통해, 정답 레이블링이 없는 상황에서 유사한 데이터셋을 하나의 Subset으로 효과적으로 묶어낼 수 있다. 다만, 클러스터의 수(K)는 사용자가 지정해주어야 하는 하이퍼파라미터로 사용자 판단하에 최적값을 모델에 집어넣어주어야 한다. 보통 최적 클러스터 수는 엘보우 방법(Elbow Method)에 따라 선택하며, 관련 내용은 아래의 게시글과 같다.
[ML] 엘보우 메소드 (Elbow method)
엘보우 메소드(Elbow Method)위키피디아의 정의를 인용하자면, 엘보우 메소드는 군집 분석(Clustering)에서 데이터 셋의 클러스터 수를 결정하는 데 사용되는 휴리스틱(heuristic) 방법입니다. 휴리스틱(h
ymechanics.tistory.com
2. 클러스터 내 분산(Within-Cluster Variation, WCV)
K-means Clustering은 각 클러스터 내에서 데이터가 최대한 서로 가깝게 되도록 하기위해, 클러스터 내 분산을 최소화한다. 분산은 데이터가 평균을 중심으로 얼마나 퍼져있는지를 나타내는 지표로, 분산이 작다는 것은 데이터가 평균 근처에 잘 몰려있다는 것을 의미한다. 따라서 클러스터 내 분산이 최소가 될때, 군집화가 잘되었다고 판단할 수 있는 것.
보통 최적제어든 강화학습이든 목적함수(또는 비용함수)를 설정해두고 이를 최소화(혹은 최대화)하는 방향으로 학습을 하게되는데, 그런 맥락에서 본다면 WCV는 K-means Clustering의 목적함수라고 볼 수도 있겠다. 따라서 K-means Clustering을 통해 풀고자 하는 문제는 아래와 같으며

보통 유클리디안 거리(Euclidean Distance)를 사용하여 WCV를 정의한다.

여기서 Ck는 k번째 클러스터를, ㅣCkㅣ는 k번째 클러스터에 속한 데이터의 수를, i' 인덱스의 데이터는 Centroid를 의미한다. 즉, K-means Clustering은 전체 Observation을 K개의 클러스터로 분할하되, 모든 클러스터의 내부 분산의 합이 최소가 되도록 하는 알고리즘이다.

3. 알고리즘(Algorithm)
K-means Clustering 알고리즘을 정리해보면 다음과 같다.

3-1. 초기 군집 할당
관측치(혹은 데이터)(Observation) 각각에 1부터 K(지정한 클러스터 수)까지 임의의 번호를 할당한다. 해당 번호가 각 관측치에 대해 초기 군집(클러스터)으로 사용된다. 각 관측치는 적어도 하나의 클러스터에 속하며[1], 모든 관측치는 반드시 하나의 클러스터에만 속해야한다[2].


3-2. 군집 중심(Centroid) 계산
K개 클러스터 각각에 대해, 해당 클러스터에 속한 관측치들의 p개 특성(Feature)에 대한 평균으로 구성된 벡터를 구한다. 해당 벡터가 곧 k번째 클러스터의 중심(Centroid)가 된다.
3-3. 재할당
각 관측치별 유클리디안 거리(Euclidean Distance)를 계산하여 가장 가까운 클러스터에 재할당한다.
3-4. 반복(Iteration)
3-2와 3-3을 수렴할 때 까지 반복한다.
이를 정리한 Pseudo Code는 다음과 같다.


4. 성질(Properties)
K-means Clustering의 대표적은 성질들을 정리해보면 아래와 같다.
1. 각 단계별 목적 함수(WCV)의 감소를 보장
2. 초기 조건의 영향으로 전역해를 보장하지 않음.

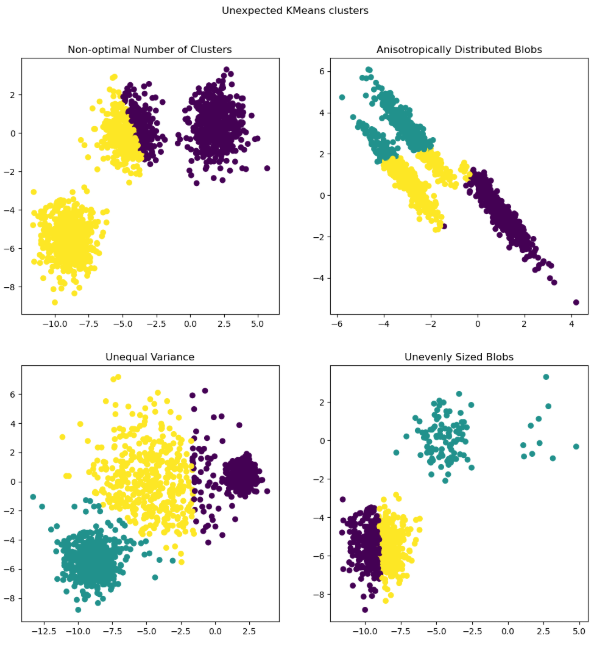
3. 비구형(Non-Globular) 데이터 혹은 밀도 & 크기 차이가 큰 데이터의 분류에 약함.

그외에도 여러 한계점들이 있다.
5. K-means Clustering 구현하기
K-means Clustering의 구현을 위해 위의 Pseudo Code를 참고하여 함수나 클래스를 짜볼 수 있겠지만, 대부분 그렇듯 누군가 만들어둔 모듈을 활용해 손쉽게 구현이 가능하다. 가장 대표적으로 sklearn의 KMeans 함수를 활용할 수 있다.
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters, random_state)
kmeans.fit(X)sklearn.cluster에서 임포트해올 수 있고, 전달인자로 클러스터 수와 시드 값을 넣어주면 손쉽게 사용이 가능하다. 초기에 랜덤하게 군집화를 진행하는 것은 맞지만 random_state=4 와 같이 특정 값을 지정해주면, 랜덤하게 할당하는 것을 고정시켜 활용하겠다는 의미이다. 따라서 이를 활용해 간단하게 구현한 K-means Clustering은 아래와 같다.
# Module import
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs, make_circles, make_moons
plt.rcParams['font.family'] = 'Times New Roman'make_blobs, make_circles, make_moons 는 원하는 모양에 맞게끔 데이터 셋을 랜덤하게 생성해주는 함수다. 3가지 예시를 통해 K-means Clustering의 성질을 확인해볼 수 있다.
X, y = make_blobs(n_samples=300, centers=3, cluster_std=1.0, random_state=42)
kmeans = KMeans(n_clusters=3, random_state=42)
kmeans.fit(X)
labels = kmeans.labels_
plt.scatter(X[:, 0], X[:, 1], c=labels)
plt.title("K-means Clustering", fontsize=20)
plt.xlabel("Feature 1", fontsize=16)
plt.ylabel("Feature 2", fontsize=16)
plt.show()
X_circles, y_circles = make_circles(n_samples=300, factor=0.5, noise=0.05, random_state=42)
kmeans_circles = KMeans(n_clusters=2, random_state=42)
kmeans_circles.fit(X_circles)
labels_circles = kmeans_circles.labels_
plt.scatter(X_circles[:, 0], X_circles[:, 1], c=labels_circles)
plt.title("K-means Clustering", fontsize=20)
plt.xlabel("Feature 1", fontsize=16)
plt.ylabel("Feature 2", fontsize=16)
plt.show()
X_moons, y_moons = make_moons(n_samples=300, noise=0.1, random_state=42)
kmeans_moons = KMeans(n_clusters=2, random_state=42)
kmeans_moons.fit(X_moons)
labels_moons = kmeans_moons.labels_
plt.scatter(X_moons[:, 0], X_moons[:, 1], c=labels_moons)
plt.title("K-means Clustering", fontsize=20)
plt.xlabel("Feature 1", fontsize=16)
plt.ylabel("Feature 2", fontsize=16)
plt.show()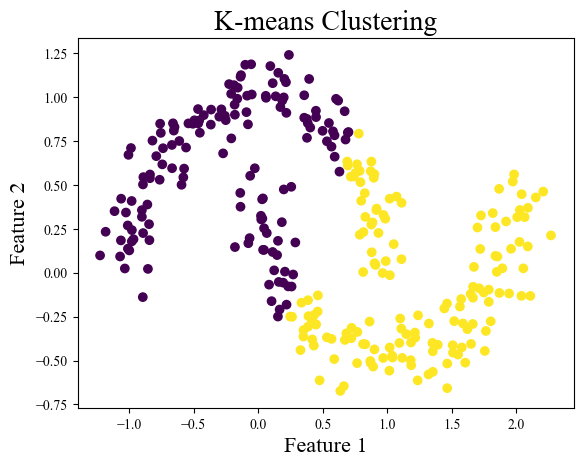
어디서든 활용하는 간단한 예시이기는 하지만, 주로 밀도, 크기에서 차이가 있거나, 구형 분포를 띄지 않는 데이터들에 대해 군집화 성능이 좋지 않은 것을 직접 확인할 수 있다. 따라서, 데이터의 특성에 따라 적절한 클러스터링 기법을 선택 & 적용할 수 있어야한다.
Reference
[1] : https://www.salientiastuff.com/k-means-clustering-part-1.html
[2] : https://www.researchgate.net/figure/K-means-Clustering-Pseudocode_fig1_371371018
[3] : https://en.wikipedia.org/wiki/K-means_clustering
[4] : https://medium.com/@atharvamanojpoonampatil/unsupervised-learning-k-means-limitations-b881f15aaae6
[5] : https://www.nb-data.com/p/why-k-means-failed-at-non-convex
[6] : https://scikit-learn.org/1.5/modules/clustering.html
'Machine Learning > Unsupervised Learning' 카테고리의 다른 글
| [ML] 비지도학습 - 차원의 저주(Curse of Dimensionality)와 차원 축소 기법(Dimensionality Reduction) (0) | 2025.04.14 |
|---|---|
| [ML] 비지도학습 - DBSCAN (0) | 2025.04.07 |
| [ML] 비지도학습 - 계층적 군집화(Hierarchical Clustering) (0) | 2025.03.31 |
| [ML] 비지도학습 - 클러스터링 개요(Clustering - Overview) (0) | 2025.03.17 |





